1. Investition in eine Immobilie vs. Alternative Investition in ein Standard-Investment

Im Aktikel Power BI Immobilien-Investitions-Analyse-Tool habe ich bereits die Idee der Performance-Messung von Immobilien-Investitionen durch die Analyse alternativer Investitionen kurz erklärt. Die Analysemöglichkeiten wurden inzwischen erweitert, weitere Simulationen wurden hinzugefügt, und ich möchte einen eigenen Blog-Artikel dazu schreiben.

Wie kann man die Performance der Immobilien-Investition messen? Beispielsweise durch Vergleich mit einem "Standard-Investment": Langfristige Renditen von Investitionen in Aktien liegen bei etwa 8 %. Da Kapitalerträge in Deutschland mit der Abgeltungssteuer besteuert werden, ziehen wir diese 25 % ab, dann landen bei einer alternativen Rendite (nach Steuern) von 6 %. Diese 6 % habe ich in meinem Power-BI-Analyse-Tool als Standardwert für i AlternativRendite %[1] hinterlegt. Natürlich kann und soll dieser Wert für individuelle Analysen angepasst werden.

Am folgenden Beispiel erkläre ich die Methode:

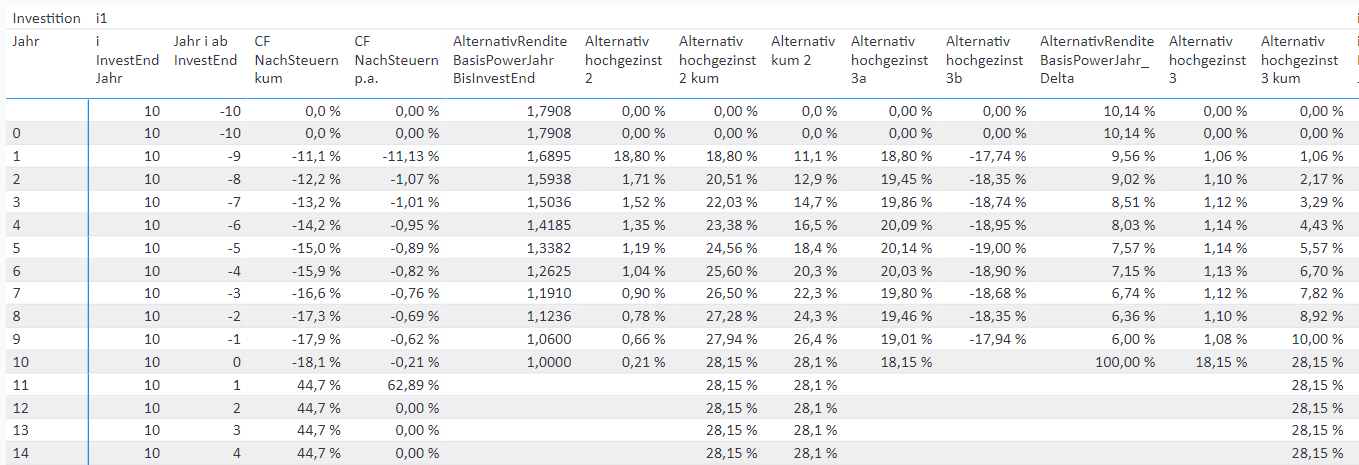
analyse alternativer investitionen 2024 04 26 15 59 53

  • Die Investition endet nach 10 Jahren ⇒ i InvestEndJahr = 10

  • CF NachSteuern kum ist der kumulierte Cashflow nach Steuern.

  • Daraus wird CF NachSteuern p.a. als der Cashflow pro Jahr berechnet.

  • AlternativRenditeBasisPowerJahr BisInvestEnd ist ein Faktor, der verwendet wird, um den Cashflow pro Jahr bis zum Ende der Investition hochzuzinsen.
    Berechnung:
    (1 + i AlternativRendite %[1]) ^ (- Jahr i ab InvestEnd)

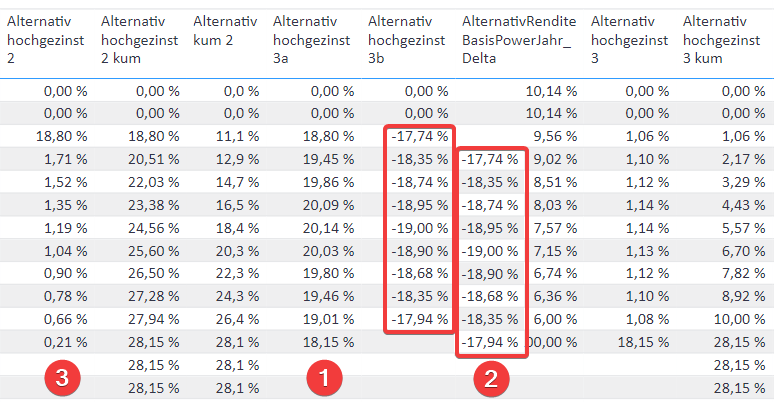
  • Alternativ hochgezinst 2 = CF NachSteuern p. a. * AlternativRenditeBasisPowerJahr BisInvestEnd
    Das ist die Kernidee der Methode:
    Der jährliche Cashflow nach Steuern wird bis zum Ende der Investition hochgezinst.

  • Alternativ hochgezinst 2 kum - Kumulation von Alternativ hochgezinst 2 bis zum Ende der Investition, denn uns interessiert ein Wert für die ganze Investition.

  • optional:
    Alternativ kum 2 = [Alternativ hochgezinst 2 kum] / COALESCE ( [AlternativRenditeBasisPowerJahr BisInvestEnd], 1.0 )
    Diese Measure ist nur dazu da, die Anzeige eines zeitlichen Verlaufs der Entwicklung der alternativen Investition zu ermöglichen. Dabei wird Alternativ hochgezinst 2 kum wieder auf das aktuelle Jahr heruntergezinst. Warum erst hochgezinst und anschließend der kumulierte Wert heruntergezinst wird, hat vor allem Performance-Gründe.

Die Berechnung der Rendite der alternativen Investition ist sehr rechenintensiv. Daher gibt es eine Alternative mit doppelter Performance: Alternativ hochgezinst 3 kum, die mathematisch am Ende der Investition zum gleichen Ergebnis führt, wie Alternativ hochgezinst 2 kum.
Allerdings ist der Wert nur am Ende der Investition korrekt. Eine Auswertung in den Jahren vor Ende der Investition ist nicht zulässig.

Anmerkung
 Um die Investition in die Immobilie mit der alternativen Investition zu vergleichen, berechnen wir:
Outperformance VVÜ CF kum[2] = [VVÜ + CF kum][3] - [Alternativ hochgezinst kum]


Die Mathematik von Alternativ hochgezinst 3

Für technisch Interessierte:

Die Performance-Steigerung der Berechnung von Alternativ hochgezinst 3 gegenüber Alternativ hochgezinst 2 basiert darauf, dass CF NachSteuern p.a. von CF NachSteuern kum abgeleitet wird. In jedem CF NachSteuern p.a. sind zwei Berechungen von CF NachSteuern kum enthalten. Das bedeutet, dass in Alternativ hochgezinst 2 kum jedes CF NachSteuern kum pro Jahr einmal mit positivem und einmal mit negativem Vorzeichen enthalten ist.

  • Alternativ hochgezinst 3 basiert direkt auf CF NachSteuern kum
    zu Demonstrationszwecken sieht man in der Tabelle, wie sich Alternativ hochgezinst 3 aus zwei einzelnen Measures zusammensetzt:

    • Alternativ hochgezinst 3a = - [CF NachSteuern kum] * [AlternativRenditeBasisPowerJahr BisInvestEnd]

    • Alternativ hochgezinst 3b = [CF NachSteuern kum] * [AlternativRenditeBasisPowerJahr BisInvestEnd-1]

  • somit gilt

    • Alternativ hochgezinst 3 = [Alternativ hochgezinst 3a] + [Alternativ hochgezinst 3b]

    • Alternativ hochgezinst 3 = - [CF NachSteuern kum] * [AlternativRenditeBasisPowerJahr_Delta]

Hier versuche ich einmal die Mathematik zu erklären:

analyse alternativer investitionen 2024 04 26 16 25 15

Man kann sich das so vorstellen, dass die Werte in der Spalte Alternativ hochgezinst 3b eigentlich eine Zeile nach untern verschoben werden müssten. Und wenn man dann rechnet: (1) + (2), dann entspricht das (3).

Das erklärt, warum am Ende der Investition die Werte von Alternativ hochgezinst 3 und Alternativ hochgezinst 2 gleich sind.

Hier der Performance-Vergleich der Berechnungen: die erste Matrix enthält Alternativ hochgezinst 3 kum, die zweite Alternativ hochgezinst 2 kum

analyse alternativer investitionen 2024 04 26 16 50 46
analyse alternativer investitionen 2024 04 26 16 49 05

Interessant ist nun, dass sich die Performance nur unwesentlich verschlechtet, wenn Alternativ hochgezinst 3 kum für sehr viele Werte parallel berechnet wird (die Tabelle hat 101 Zeilen).

analyse alternativer investitionen 2024 04 26 16 57 12
analyse alternativer investitionen 2024 04 26 16 57 52

Die Tabelle benötigt mit 34 Sekunden zwar fast doppelt so lange, wie die zweite Matrix. Aber die Tabelle enthält nicht einfach nur Alternativ hochgezinst 3 kum, sondern
Outperformance VVÜ CF kum[2] = VVÜ + CF kum[3] - [Alternativ hochgezinst kum]

2. Simulations-Tabellen für Outperformance VVÜ CF kum

Wie die oben beschriebenen Performance-Tests gezeigt haben, kann Outperformance VVÜ CF kum[2] auch parallel für einen ganzen Bereich von i AlternativRendite %[1] oder für andere Serien berechnet werden. Somit kann nicht nur die Frage beantwortet werden:

  • Wieviel besser (oder schlechter) ist eine konkrete Investition in Immobilien im Vergleich zu einer alternativen Investition mit der Standard-i AlternativRendite %[1] von 6 %?

Wir können auch solche Fragen beantworten:

  • Welche i AlternativRendite %[1] benötigt eine alternative Investition, um das gleiche Ergebnis zu erzielen, wie die Immobilien-Investition?

  • Welche i Wertsteigerung_1 %[4] benötigen die Investitionen, damit sie das gleiche Ergebnis zu erzielen, wie alternative Investitionen mit der Standard-i AlternativRendite %[1] von 6 %?

  • Wie wirkt sich die Mietrendite i Rendite % p0[5], i Fremdkapital %[6], Zinssatz, Tilgungssatz und andere Parameter auf die Outperformance VVÜ CF kum[2] aus?

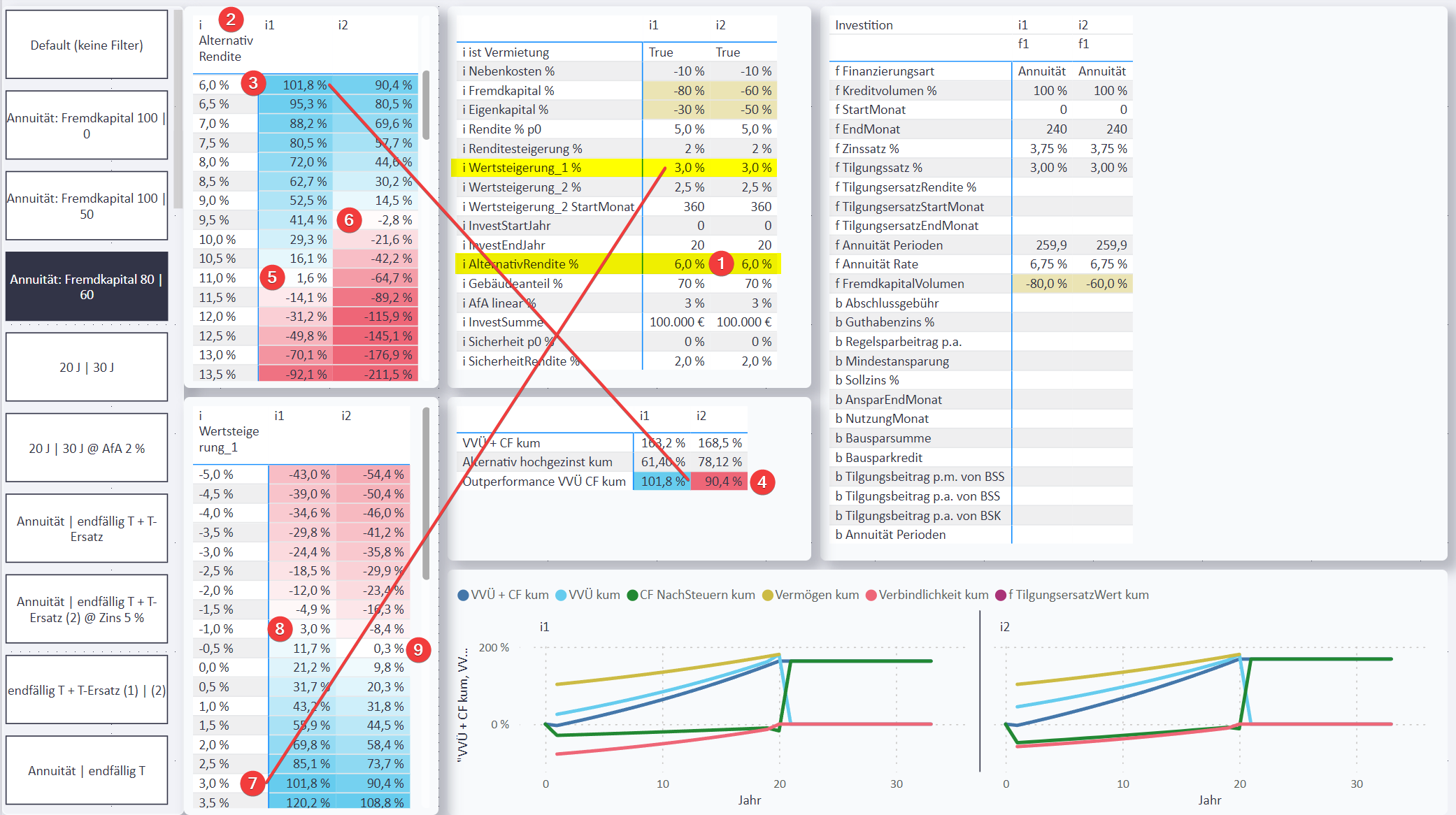
performance messung von immobilien investitionen 2024 04 29 15 13 02

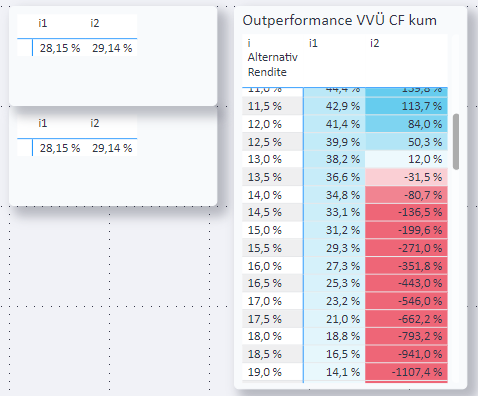
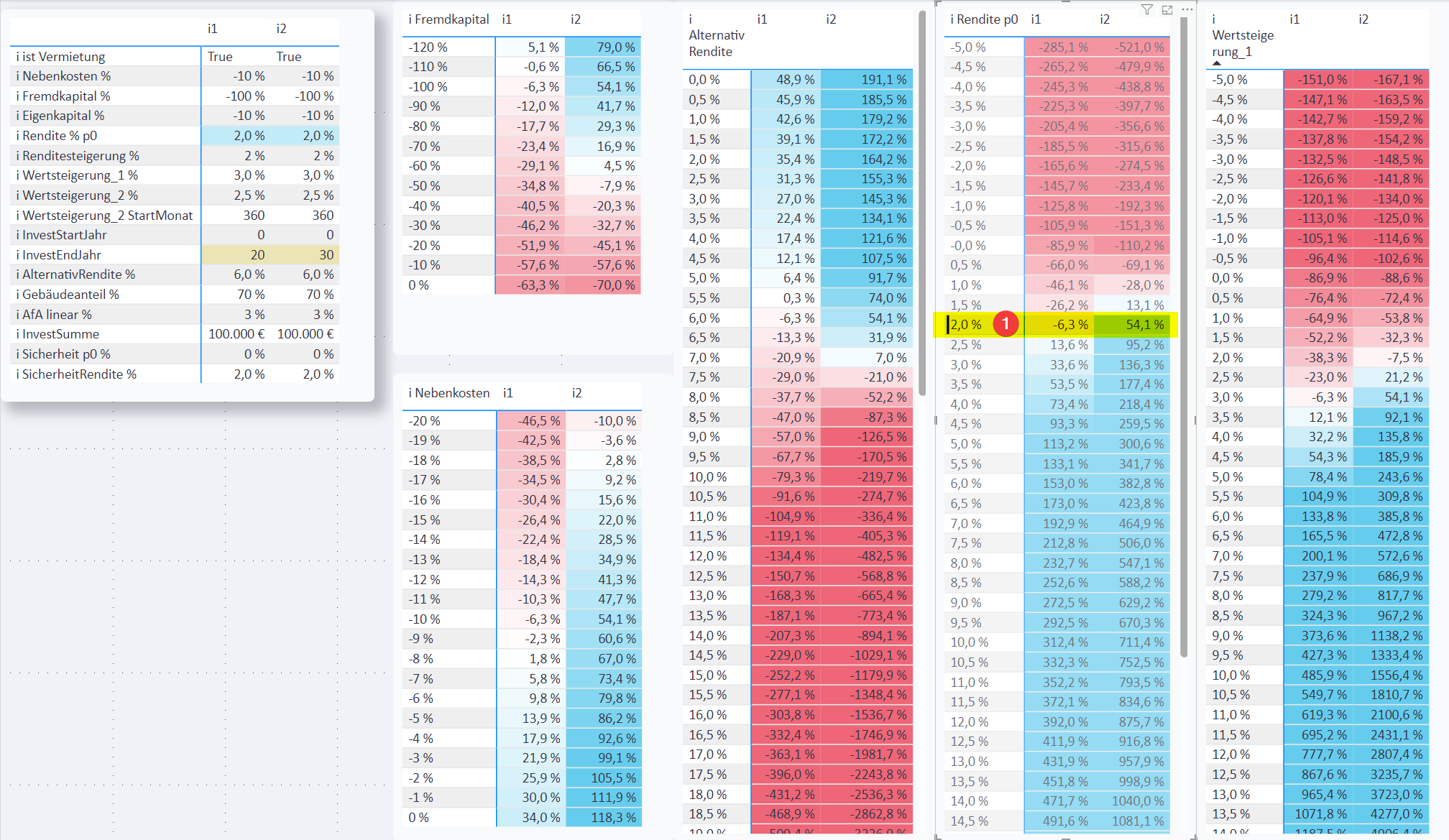
Hier der Vergleich von zwei Investitionen: i1 mit 80 % Fremdkapital, i2 mit 60 % Fremdkapital:

  1. Der Standard-Wert für i AlternativRendite %[1] ist 6,0 %.

  2. In dieser Tabelle gibt es die berechneten Werte von Outperformance VVÜ CF kum[2] für unterschiedliche i AlternativRendite %[1].

  3. Die Zeile für i AlternativRendite %[1] = 6,0 % representiert den Standard-Wert.

  4. Diese Werte von Outperformance VVÜ CF kum[2] für die Standard-i AlternativRendite %[1] werden immer auch separat in dieser Ergebnis-Tabelle angezeigt und erlauben eine schnelle und standardisierte Bewertung der Investitionen.

  5. Welche i AlternativRendite %[1] müsste für die Investition i1 angenommen werden, damit es ein Gleichgewicht zwischen VVÜ + CF kum[3] und Alternativ hochgezinst kum gibt?
    Wann geht Outperformance VVÜ CF kum[2] gegen 0?
    Bei i1 müsste i AlternativRendite %[1] etwa 11,0 % sein

  6. Bei i2 müsste i AlternativRendite %[1] etwa 9,5 % sein

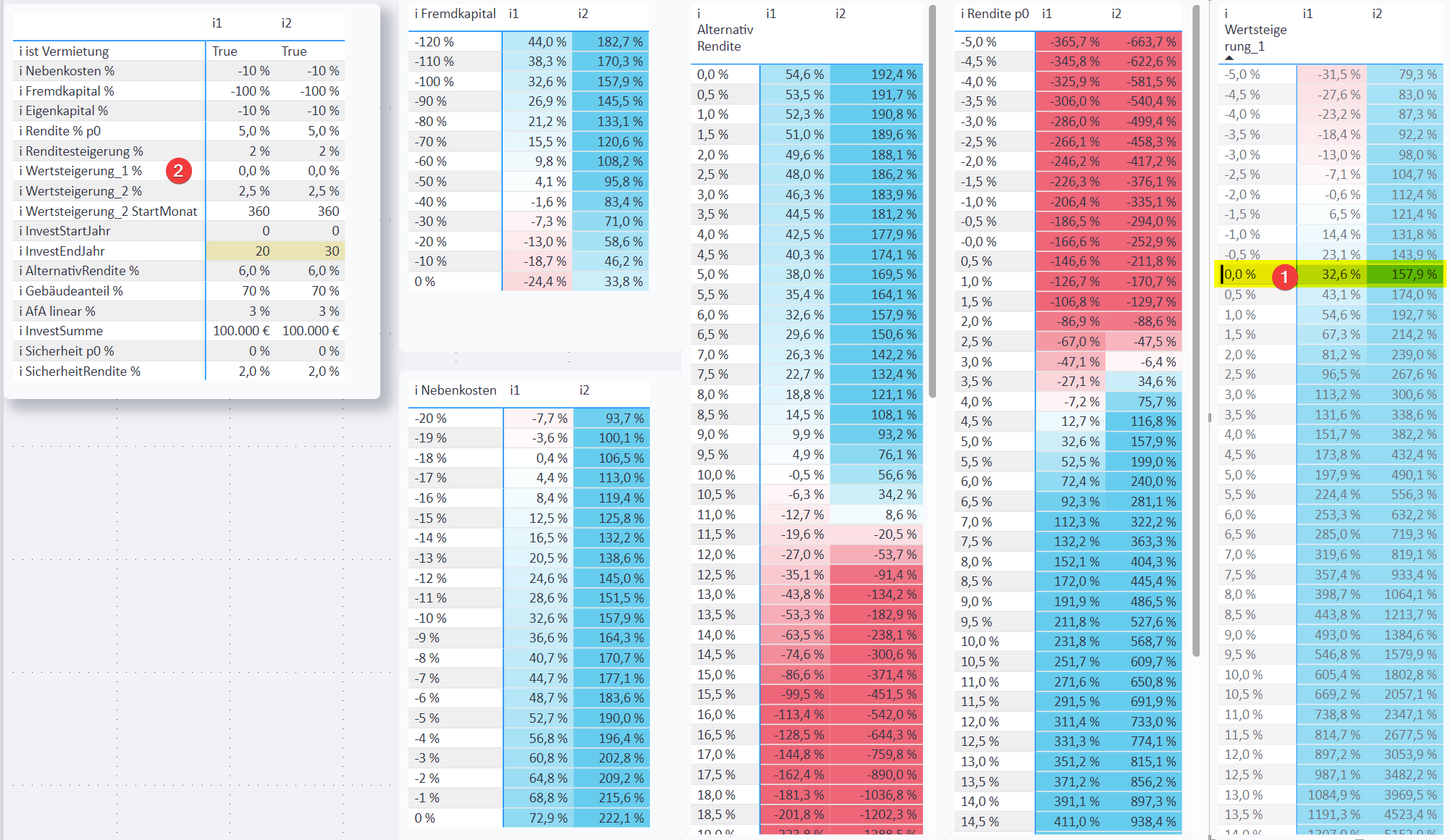
  7. Auch der Einfluss der i Wertsteigerung_1 %[4] auf Outperformance VVÜ CF kum[2] wird analysiert.
    In dieser Zeile sehen wir die Berechnung für die Standard-i Wertsteigerung_1 %[4] von 3,0 %
    Dabei wird der für i AlternativRendite %[1] der Standardwert von 6,0 % verwendet.

  8. Bei welcher i Wertsteigerung_1 %[4] geht Outperformance VVÜ CF kum[2] gegen 0?
    Bei i1 müsste i Wertsteigerung_1 %[4] mindestens -1,0 % sein, bei einer höheren i Wertsteigerung_1 %[4] lohnt sich die Investition im Vergleich zur Alternative.

  9. Bei i2 müsste i Wertsteigerung_1 %[4] mindestens -0,5 % sein, damit die Investition besser als die Alternative ist.

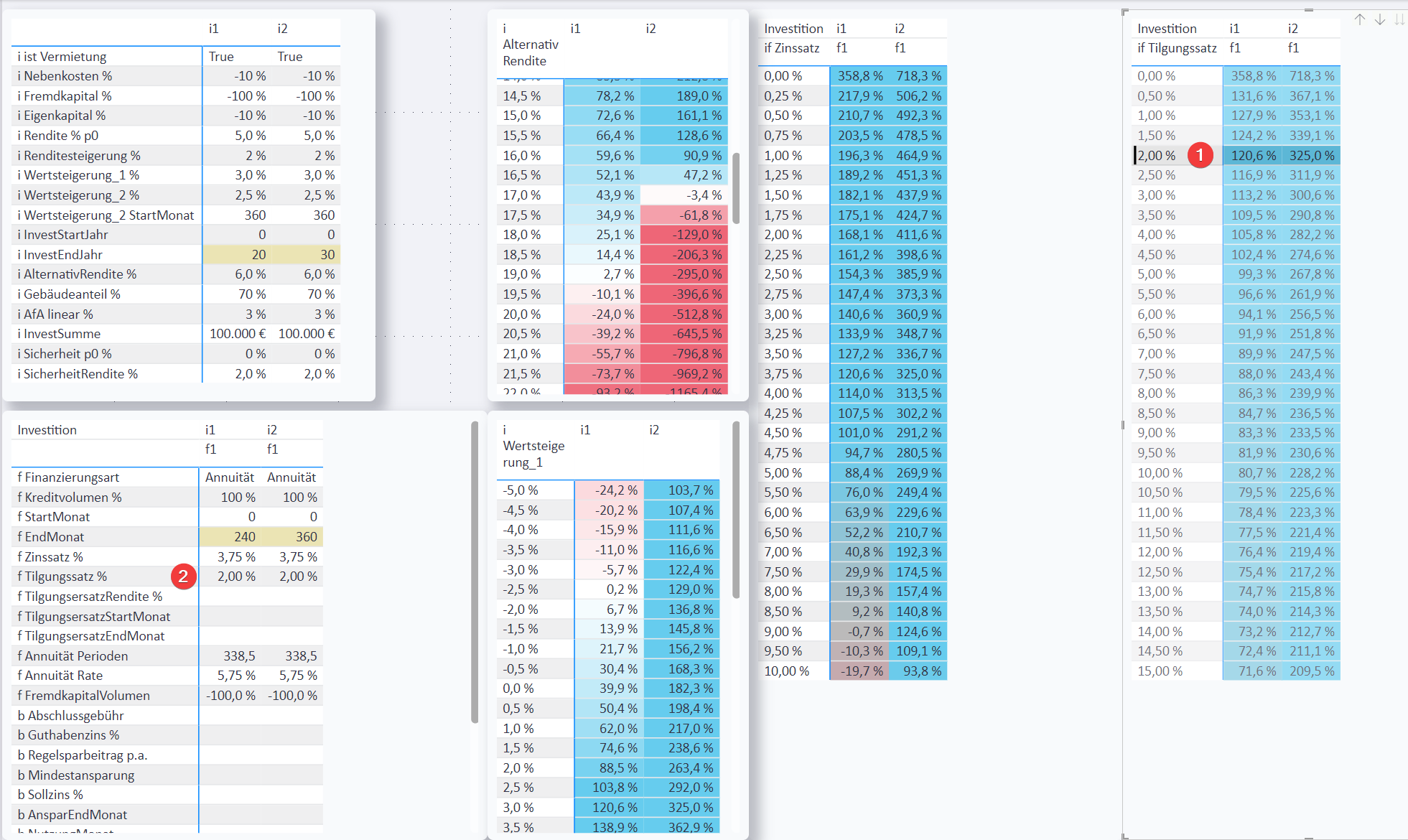
3. Schnell-Simulationen geänderter Investitions- und Finanzierungs-Parameter

Es gibt es weitere Seiten für andere Simulationen:

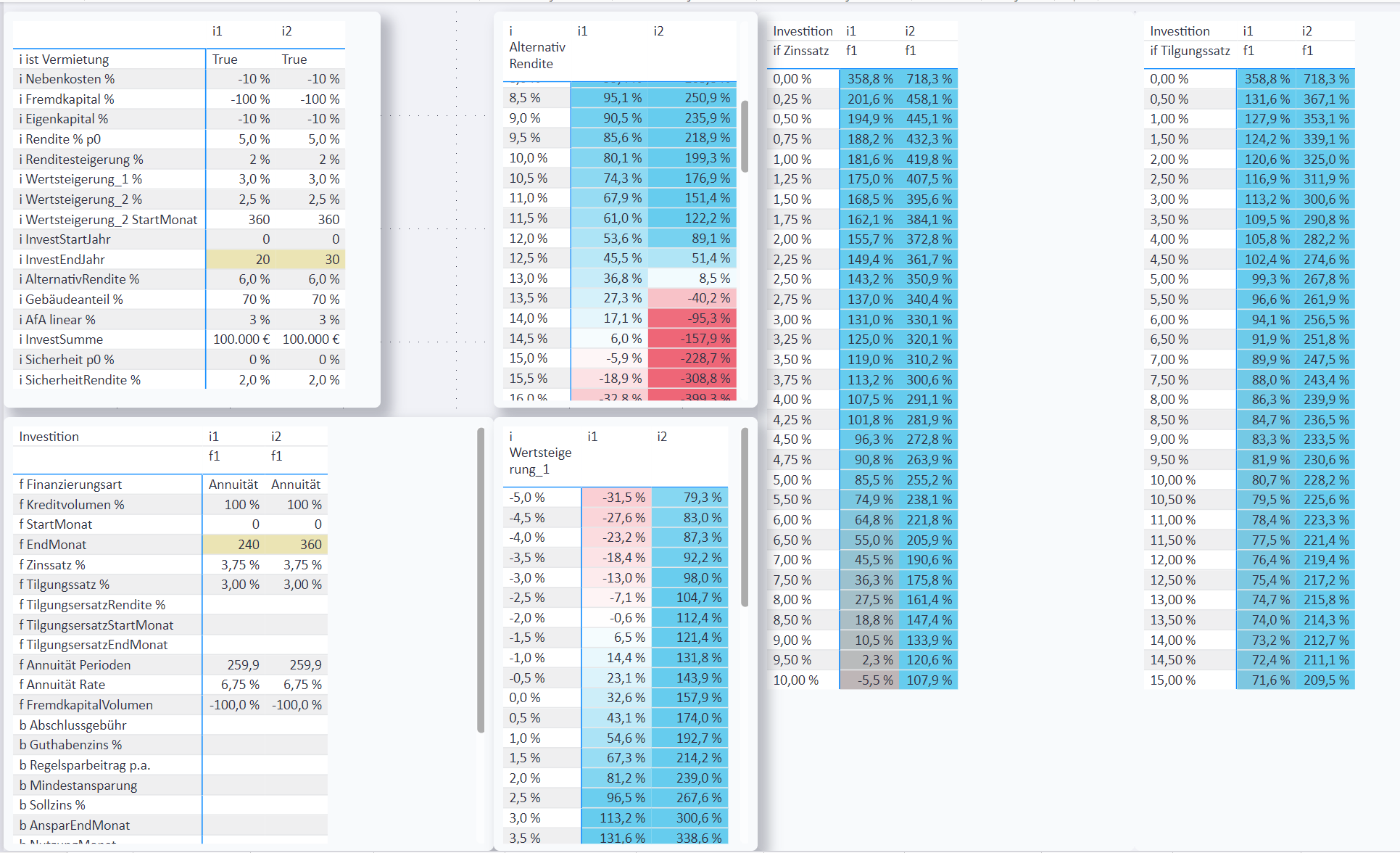
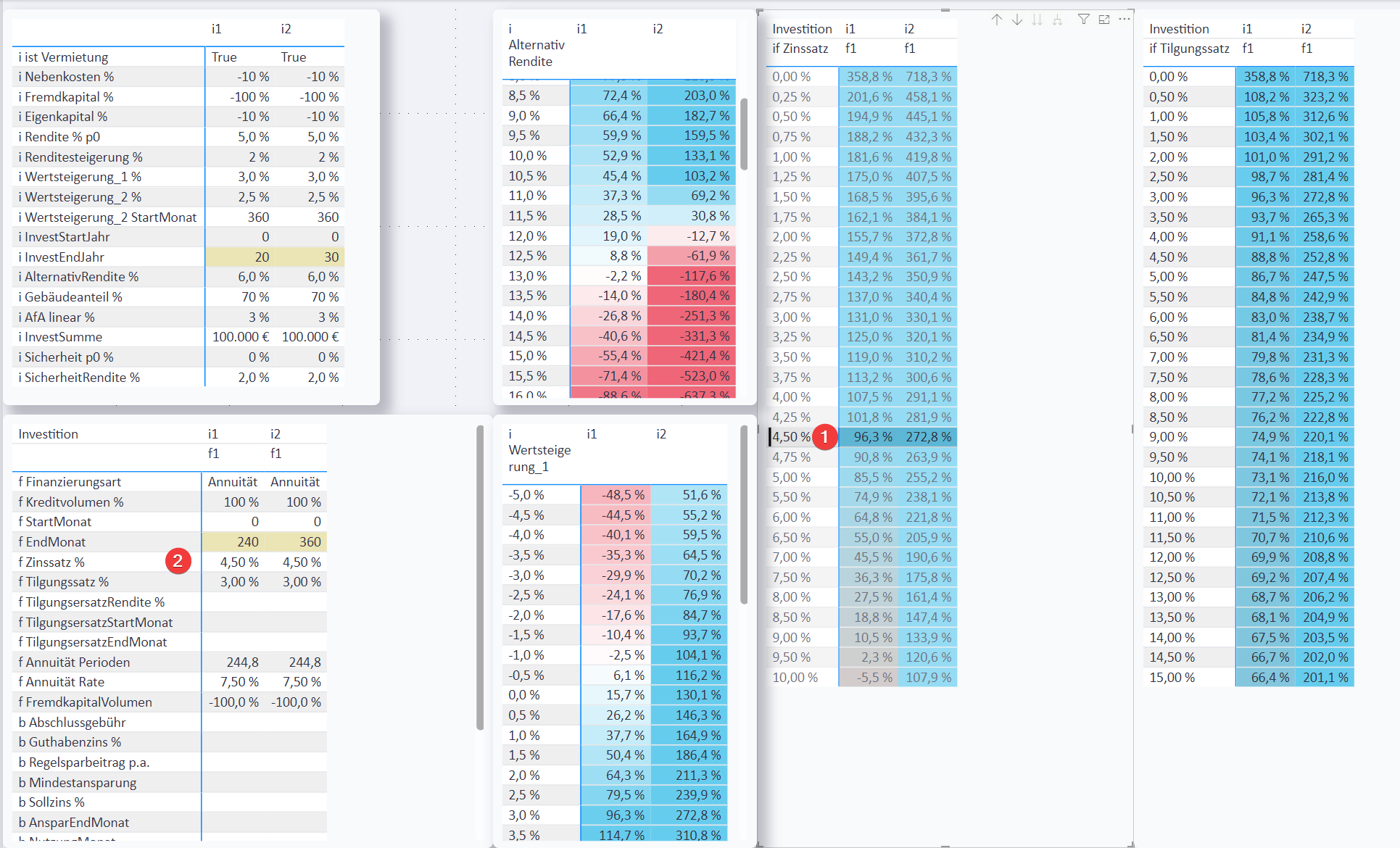
Hier der Vergleich einer Investition mit Annuitäten-Darlehen[7] über 20 oder 30 Jahre:

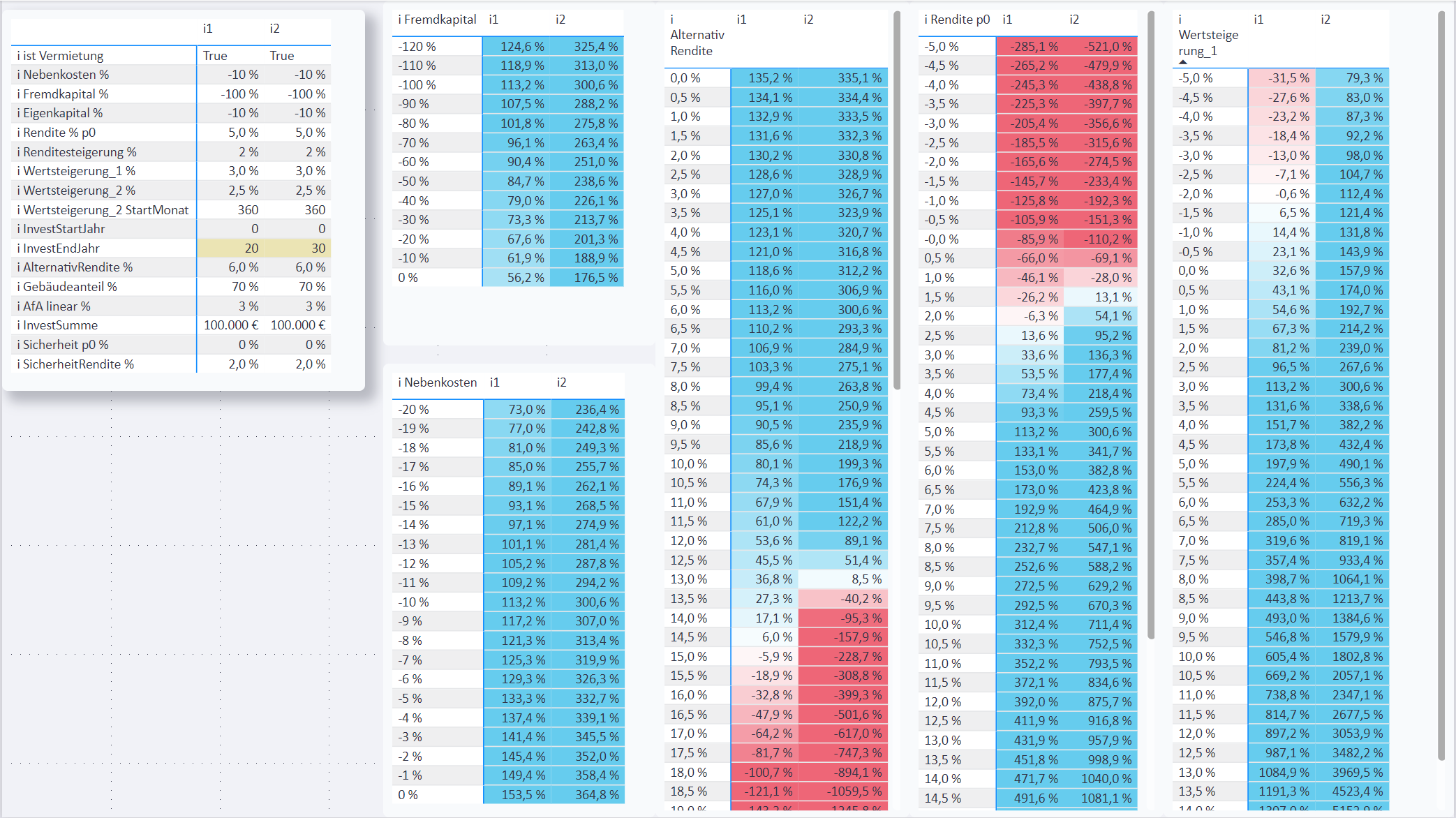
performance messung von immobilien investitionen 2024 04 29 15 25 36

Auf dieser Seite sind insbesondere interaktive Schnell-Simulationen für verschiedene Werte aus den verschiedenen Tabellen möglich. Man braucht nur eine Zeile oder einen Wert anklicken, und schon werden die angeklickten Inhalte als Parameter übernommen und bilden die Grundlage der Berechnung der anderen Tabellen.

Beispiele:

Beispiel 1. Wie würde sich eine geringere Mietrendite von 2,0 % auswirken?
performance messung von immobilien investitionen 2024 04 29 15 29 09
Beispiel 2. Wie würde sich eine Wertsteigerung von 0 % auswirken?
performance messung von immobilien investitionen 2024 04 29 15 34 36

Auch Finanzierungsparameter lassen sich in Simulationen verwenden.

performance messung von immobilien investitionen 2024 04 29 15 51 58
Beispiel 3. Wie würde sich eine höherer Zinssatz von 4,50 % auswirken?
performance messung von immobilien investitionen 2024 04 29 15 53 45
Beispiel 4. Wie würde sich eine geringerer Tilgungssatz von 2,00 % auswirken?
performance messung von immobilien investitionen 2024 04 29 16 03 45

4. Über mich

Görtz-Invest: Ihre Investition in Wohnimmobilien mit Fremdkapital.
Vermittlung der Finanzierung von Wohnimmobilien ("Baufinanzierung"), Ratenkrediten, Immobilien als Kapitalanlage, Investitionen in Wertpapiere

Tipp
 YouTube Kanal "Der Immobilien-Investor"

Tipp
 kostenloser online-Kurs "Grundlagen der Baufinanzierung: Konzepte, Wissen, Expertentipps"

Tipp
 Als exklusiven Bonus biete ich für meine Baufi-Coaching-Kunden die Möglichkeit kostenloser individueller Immobilien-Investitions-Analysen mit Power-BI, wie Sie diese hier auf dieser Website sehen!


1. 'i AlternativRendite %': Rendite einer angenommenen alternativen Investition, wenn der Cashflow der Investition ('CF NachSteuern kum') alternativ investiert würde, beispielsweise in Aktien.
2. 'Outperformance VVÜ CF kum': die Outperformance der Kennzahl 'VVÜ + CF kum' gegenüber 'Alternativ kum'. Insbesondere diese Kennzahl dient in unseren Szenarien und Konzepten der Bewertung einer Investition und ist daher in der Tabelle farblich hinterlegt, um die beiden Investitionen 'i1' und 'i2' sofort optisch vergleichen zu können. Je geringer dabei der Wert für 'Alternativ kum' ist, umso besser, denn das entspricht einem geringeren benötigten Cashflow.
3. 'VVÜ + CF kum': Summe aus 'VVÜ kum' (kumulierter Vermögen-Verbindlichkeit-Überschuss) und 'CF kum' (kumulierter Cashflow)
4. 'i Wertsteigerung_1 %': jährliche Wertsteigerung der Investition. Von 'i InvestStartMonat' bis 'i InvestEndMonat' oder bis 'i Wertsteigerung_2 StartMonat'
5. 'i Rendite % p0': jährliche Rendite der Investition (durch Vermietung) in der Periode 0, also zu Beginn der Investition. In Abhängigkeit von 'i Renditesteigerung %' erhöht sich die Rendite jährlich. Der Parameter wird auch für selbstgenutzte Immobilien verwendet, hat dabei aber eine andere Bedeutung: Es ist die eingesparte Miete, die der Eigentümer für ein anderes analoges Objekt bezahlen müsste, wenn er seine Immobilie nicht selbst nutzen würde.
6. 'i Fremdkapital %': Das eingesetzte Fremdkapital als Prozentsatz von der Investition. Fremdkapital ist ein Kredit, der von Dritten bereitgestellt wird und vom Kreditnehmer zurückgezahlt werden muss.
7. Annuität: Ein Annuitätendarlehen ist ein Tilgungsdarlehen mit konstanten Rückzahlungsbeträgen (Raten). Dabei bleibt die Höhe der zu zahlenden Rate über die gesamte Laufzeit gleich (zumindest während der vereinbarten Zinsbindungsfrist). Die Annuitätenrate oder kurz Annuität setzt sich aus einem Zins- und einem Tilgungsanteil zusammen. Da mit jeder Rate ein Teil der Restschuld getilgt wird, verringert sich der Zinsanteil zugunsten des Tilgungsanteils. Am Ende der Laufzeit ist die Kreditschuld vollständig getilgt. Der Zinssatz wird bei Abschluss eines Annuitätendarlehens über einen vertraglich vereinbarten Zeitraum festgeschrieben. Dieser Zeitraum kann sich auch über die komplette Kreditlaufzeit erstrecken. Es handelt sich dann um einen Voll-Tilger.